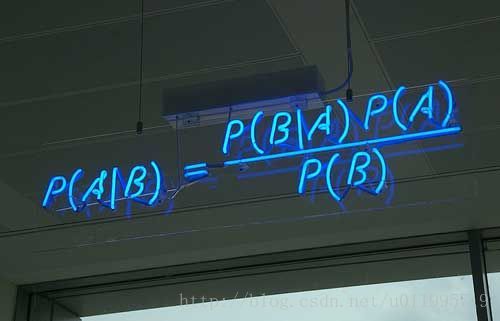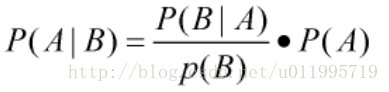统计学中，在探讨 不确定性（概率） 这件事时分两派:频率学派和贝叶斯学派。
频率学派认为概率是事件在长时间内发生的频率，是固定的。（比如我们若何得知抛一枚硬币出现正面的概率是0.5，这是通过抛了好多好多次之后，我们统计正面出现频率发现是0.5，那就认为抛一枚硬币出现正面的概率是0.5，注意，这里是必须抛好多好多次之后，我们才能得到概率）贝叶斯学派认为概率是被解释为我们对一件事情发生的相信程度，即对此事件发生的信心。而对此事件发生的信心（概率）是会变化的，是随着我们不断获得新的信息而发生变化。
举个例子，一枚硬币我抛第0次，我们是无法知道出现正面的概率是多少的，抛了10次，出现了9次正面，1次反面，我们就认为，硬币出现正面的概率是0.9，当抛第11次的时候，我们看到出现的是正面（这个信息就是 获得的新信息），那么我们就会对硬币出现正面这个事件发生的信心（概率）作出变化，认为是概率是10/11。
扯远了，这两天在重温贝叶斯公式，找了不少资料，对贝叶斯有了新的认识，而且看了不少优秀的博客，里边的观点给我新的启发，于是乎打算写个blog记录一下。
在这里，先讲两个概念，
先验概率(prior probability）是指根据以往经验分析得到的概率后验概率（posterior probability）是指在得到“结果”的信息后重新修正的概率
看看后验概率的解释是不是很熟悉？贝叶斯学派就是这么确定一个事件发生的概率的啊 ！ 得到“结果”的信息 对应 获得新的信息，重新修正的概率就是后验概率，
后验概率就是我得到了一些新消息之后对原来的概率（先验概率）进行“修正”。 后验概率就是修正了的先验概率。 后验概率就是对先验概率进行修正后得到的概率值。看不懂没关系，知道有先验概率和后验概率就好，后边会解释清楚。
先膜拜一下贝叶斯：
再膜拜一下贝叶斯公式：
（大学考试时，就死记硬背这个公式，把后面的（B）放分母，前面的（A）放分子，分子再乘一项这个的交换（A\B）变成（B\A））方便快捷。。。然而这样完全丢失了伟大的贝叶斯思想。
解释贝叶斯公式最简单的方法就是举栗子，举栗子，举栗子
（举栗子之前，定义一下先验概率，后验概率，修正因子
贝叶斯公式等号左边的就是后验概率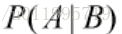
，等号右边分子的P（A）就是先验概率，剩下的那一块就是修正因子啦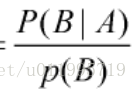
重新排一下就是：
这么讲还是很抽象，什么是后验概率？什么是先验概率？什么是修正因子？
栗子1：
大家都考过试，做过选择题（单选），而选择题的答案（通常是ABCD）往往是遵循某种分布的，譬如12道单选题中，ABCD各占3个。
那么我们来考虑一个做单项选择题的问题，假设一位同学cc，要做一份卷子，卷子如下，仅有四道单选题，每道单选题只有四个选项，并且知道四道题的答案的分布是 ABCD各一个：- 1 + 1 = （） A. 2 ; B. 8 ; C. 6 ;D. 10
- 1 + 2 = （） A. 2 ; B. 3 ; C. 6 ;D. 10
- 1 + 3 = （） A. 2 ; B. 8 ; C. 4 ;D. 10
- 甲、乙、丙、丁四人商量周末出游，甲说：乙去，我就肯定去；乙说：丙去我就不去；丙说：无论丁去不去，我都去；丁说：甲乙中至少有一个人去，我就去。以下哪项推论可能是正确的： A 乙、丙两个人去了 ； B 甲一个人去了； C 四人都去了； D 甲、丙、丁 三个人去了
请在10秒内给出这四道题的答案，没错就是ABC……（大写黑人问号脸）
第四题是什么鬼？10秒做 1+1 我就会，可是第四题。。。只能随机猜了啊。但是如果是随机猜，答对的概率是四分之一，但是有了贝叶斯公式，就可以猜得更准啦，在这里可以从25%的概率提升到100%！看cc同学是如何利用贝叶斯公式在10秒内正确答对这四道题的。 cc同学用了3秒钟完成了 1，2，3道题，得到答案分别是：A B C，然后她看到第四道题就meng了。还好她学过贝叶斯公式！经过7秒的计（xia）算（cai），第四道题她选择D 。她是如何应用贝叶斯公式的呢？ 是这样的：首先我们知道 四道题 答案分布是 ABCD各一个，在没有做1，2，3道题的时候，猜第4道题的答案，那么肯定是
P（答案=A） = P（答案=B）=P（答案=C） = P（答案=D） = 0.25 ，这个就是我们的先验知识（也称先验概率，忘记了赶紧往上拉），当cc把第1，2，3道题的答案都算出来是A B C之后，这个时候就有了新的信息，也就是 1，2，3道题的正确答案是 A B C ，那么我们再去猜第四道题。 在这里，要谨记一个前提，四道题答案分布是 ABCD各一个 这样，第1，2，3道题的答案可能的组合是 ：ABC; ACD; ABD; BCD； （这里说的是三个字母的组合，随便对应哪道题，这里并不关心，因此只有四种可能） 那么P（123 = ABC） 的概率就是 四分之一；我们直接计算 第四道题答案=D 的概率（实在不会编辑公式，手写吧）：
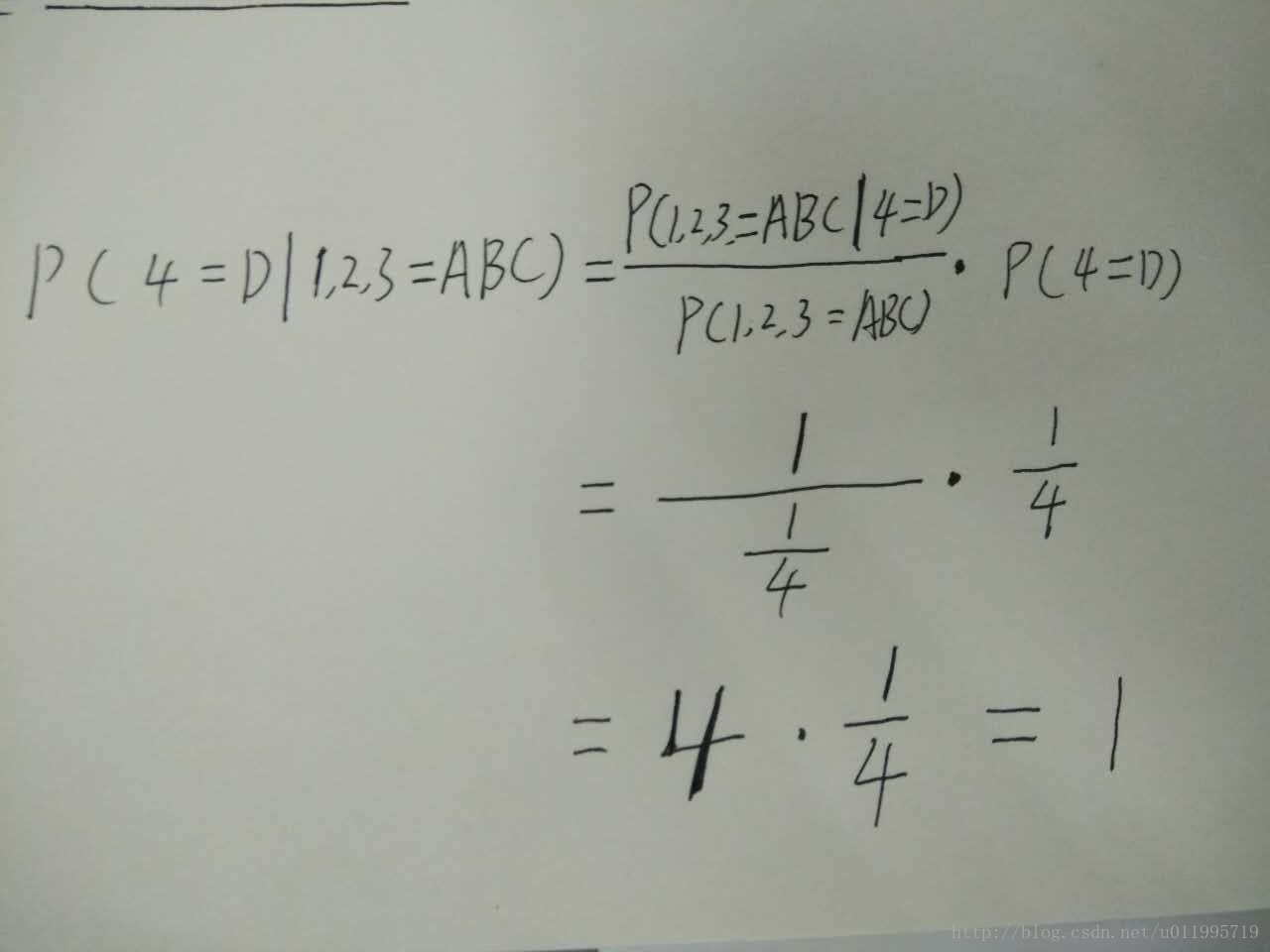
我们发现竟然直接可以得出第四道题的答案是D。
从原来的 第四题选D 的概率四分之一（先验概率），通过我们得到新的信息（123选了ABC），我们对第四道题选择D的信心（信念）进行了修改（后验概率），这就是贝叶斯的思想。